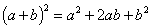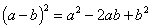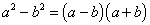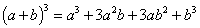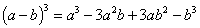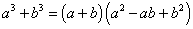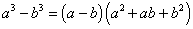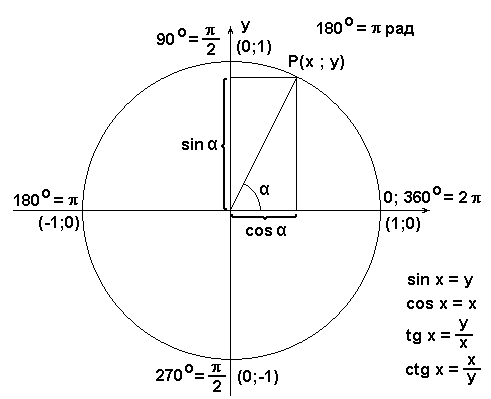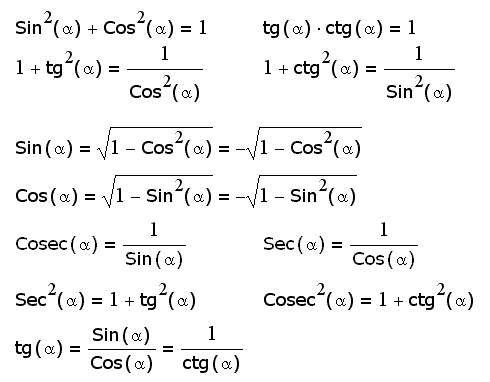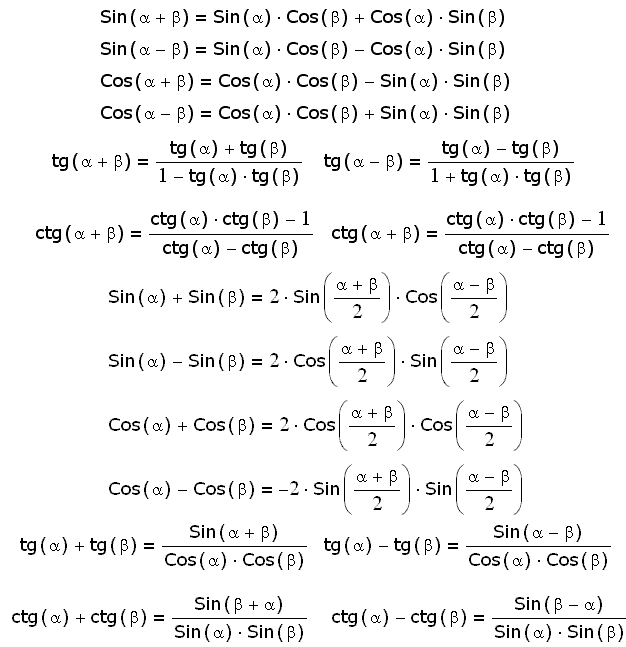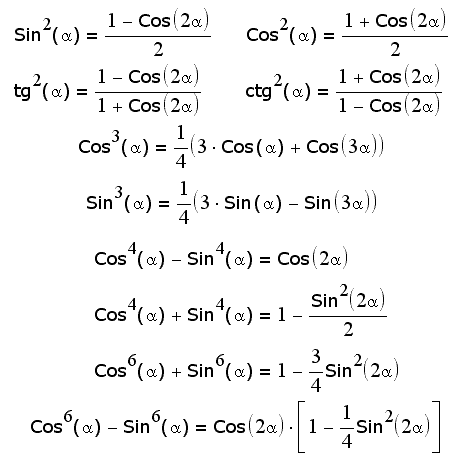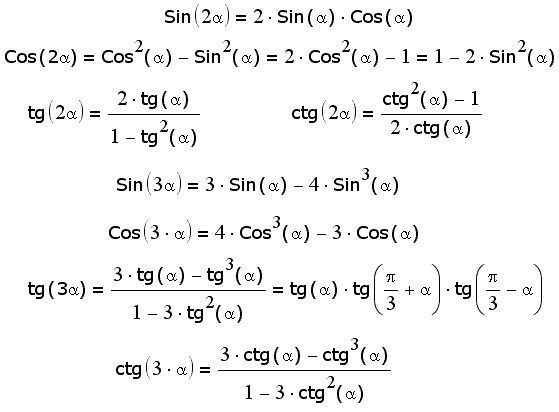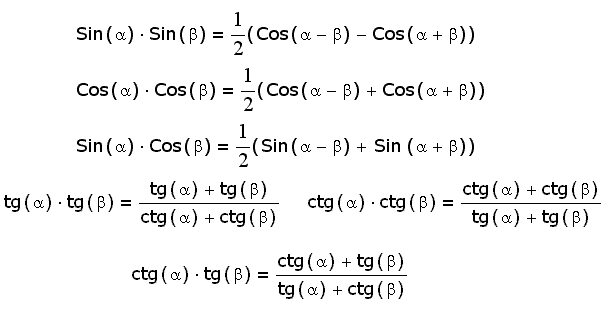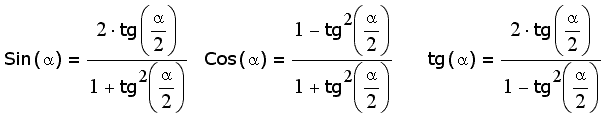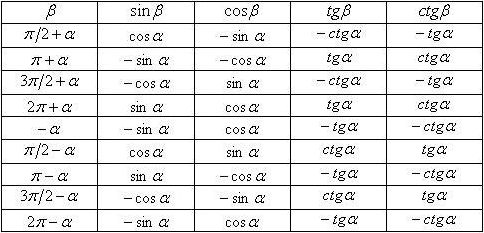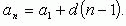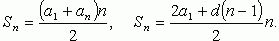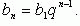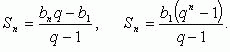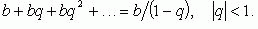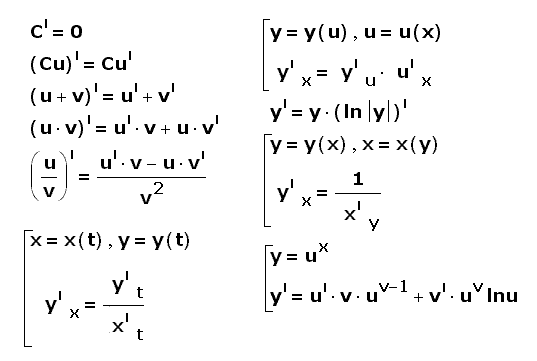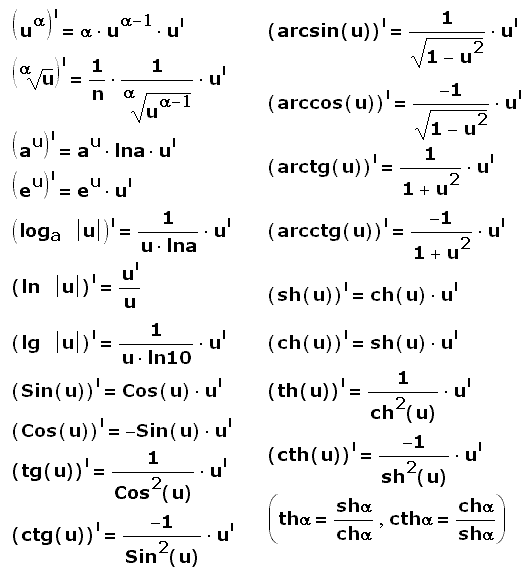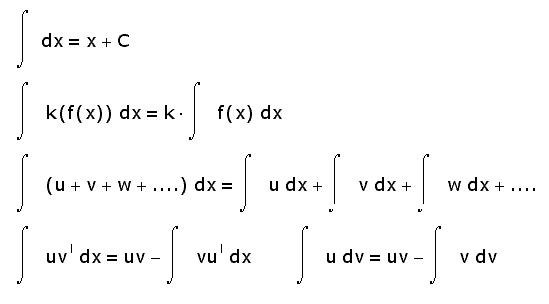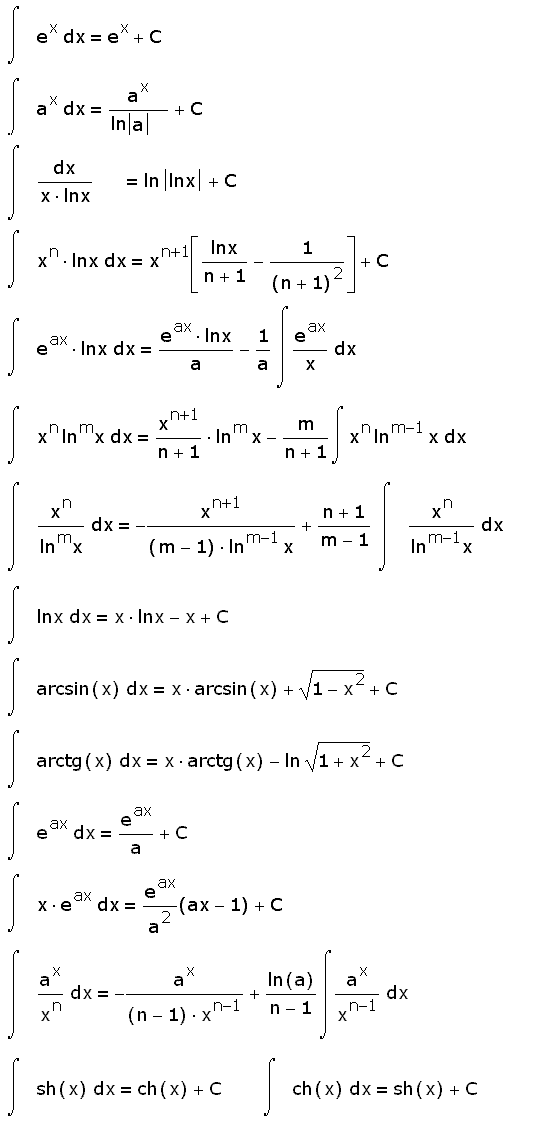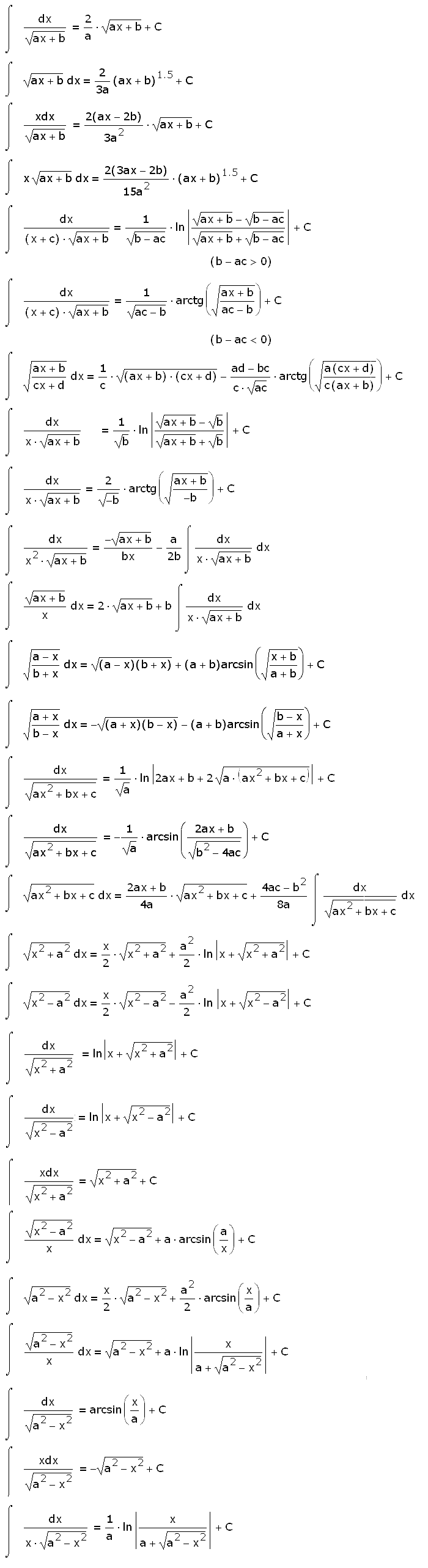Формулы

Для разложения многочленов на множители, упрощения выражений, приведения многочленов к
стандартному виду используют формулы сокращенного умножения
(часто встречающиеся случаи умножения многочленов). Все они доказываются
непосредственным раскрытием скобок и приведением подобных слагаемых. Так как формулы сокращенного умножения
применяются практически во всех задачах школьного курса математики, то их необходимо знать наизусть!

Формулы сокращенного умножения

Формулы для квадратов

Квадрат суммы:

Квадрат разности:

Разность квадратов:

Квадрат суммы: формулы сокращенного умножения

Квадрат разности: формулы сокращенного умножения

Разность квадратов: формулы сокращенного умножения

Формулы для кубов

Куб суммы:

Куб разности:

Сумма кубов:

Разность кубов:

Куб суммы: формулы сокращенного умножения

Куб разности: формулы сокращенного умножения

Сумма кубов: формулы сокращенного умножения

Разность кубов: формулы сокращенного умножения

Формулы и свойства степеней

Степень

Число с называется n-ной степенью числа а, если

Свойства и формулы степеней используются при сокращении и упрощении сложных выражений, при
решении уравнений и неравенств. Свойства степеней можно
использовать совместно с
таблицей степеней и
таблицей умножения.
В этом разделе описаны основные правила работы со степенями.

Формулы и свойства степеней

(степени с целыми показателями)

a¹ = а, a⁰ = 1 (a ≠ 0), a^-n = 1/aⁿ.

1° a^maⁿ = a^m+n;

2° a^m/aⁿ = a^m-n;

3° (ab)ⁿ = aⁿbⁿ;

4° (a^m)ⁿ = a^mn;

5° (a/b)ⁿ = aⁿ/bⁿ.

Тригонометрические формулы

Тригонометрические формулы:

Формулы, связывающие функции одного аргумента (угла) (11 шт)
Формулы суммы и разности (16 шт)
Формулы понижения степени (10 шт)
Формулы для функций кратных аргументов (11 шт)
Формулы произведения функций (6 шт)
Формулы, связывающие все тригонометрические функции с тангенсом половинного угла (3 шт)

Формулы, связывающие функции одного аргумента (угла) (11 шт)

Тригонометрические формулы, связывающие функции одного аргумента (угла)

Формулы суммы и разности (16 шт)

Тригонометрические формулы суммы и разности

Формулы понижения степени (10 шт)

Тригонометрические формулы понижения степени

Формулы для функций кратных аргументов (11 шт)

Тригонометрические формулы для функций кратных аргументов

Формулы произведения функций (6 шт)

Тригонометрические формулы произведения функций

Формулы, связывающие все тригонометрические функции с тангенсом половинного угла (3 шт)

Тригонометрические формулы, связывающие все тригонометрические функции с тангенсом половинного угла

Формулы приведения тригонометрических функций

Формулы приведения тригонометрических функций упрощают вид формул и помогают совершать преобразования,
приводящие к более простым выражениям.
Формулы приведения - приведённые ниже формулы, дающие возможность находить численные значения
тригонометрических функций углов, превышающих 90°.

Эти формулы приведения позволют избавиться от рассмотрения углов, больших 90° и отрицательных углов.

Формулы прогрессий (арифметическая и геометрическая)

Прогрессия - последовательность чисел, получаемых по некоторому правилу. Числа
составляющие последовательность, называются ее членами.

Прогрессии:

арифметическая прогрессия;
геометрическая прогрессия.

Арифметическая прогрессия

Арифметическая прогрессия - это последовательность чисел, в которой каждый член получается
из предыдущего путем прибавления к нему одного и того же числа d, называемого разностью
этой арифметической прогрессии.

Формула n-го члена:

Формулы суммы n первых членов:

Формула n-го члена: формулы прогрессий

Формулы суммы n первых членов: формулы прогрессий

Геометрическая прогрессия

Геометрическая прогрессия - это последовательность чисел, каждое из которых равно предыдущему,
умноженному на некоторое постоянное для данной прогрессии число q, называемое знаменателем этой
геометрической прогрессии.

Формула n-го члена:

Формулы суммы n первых членов:

Сумма бесконечной прогрессии:

Формула n-го члена: формулы прогрессий

Формулы суммы n первых членов: формулы прогрессий

Сумма бесконечной прогрессии: формулы прогрессий

Формулы и свойства логарифмов

Логарифмы

Логарифм числа b по основанию a (log_ab) определяется как показатель степени,
в которую надо возвести число a, чтобы получить число b (Логарифм существует только у положительных чисел).

Обозначение: log_ab.

log_ab = x, a^x = b.

Логарифм числа b по основанию a - log_ab (a > 0, a ≠ 1, b > 0)

Десятичный логарифм - lg b (Логарифм по основанию 10, а = 10).

Натуральный логарифм - ln b (Логарифм по основанию e, а = e).

Формулы и свойства логарифмов

1° Основное логарифмическое тождество - a^log_ab = b;

2° log_a1 = 0;

3° log_aa = 1;

4° log_a(bc) = log_ab + log_ac;

5° log_a(b/c) = log_ab - log_ac;

6° log_a(1/c) = log_a1 - log_ac = - log_ac;

7° log_a(b^c) = c log_ab;

8° log_(a^c)b = (1/c) log_ab;

9° Формула перехода к новому основанию - log_ab = (log_cb)/(log_ca);

10° log_ab = 1/log_ba;

Переход от выражения к логарифму называется логарифмированием этого выражения. Переход от логарифма к подлогарифмическому выражению называется потенциированием. В математике преимущественно используют натуральные логарифмы.
Свойства и формулы логарифмов незаменимы при решении логарифмических уравнений и функций, упрощении примеров, также они пригодятся при решении интегралов и нахождении производной от логарифмов.